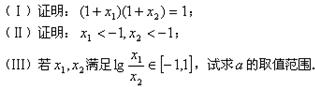如图所示，抛物线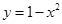
与
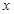轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在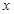轴上.已知工业用地每单位面积价值为
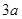元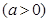
，其它的三个边角地块每单位面积价值
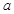元.
（1）求等待开垦土地的面积；
（2）如何确定点C的位置，才能使得整块土地总价值最大.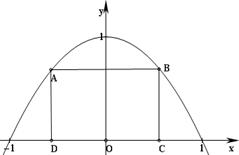
（（本小题满分12分）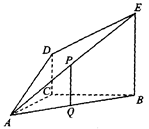
如图，DC⊥平面ABC，EB // DC，AC =BC = EB = 2DC=2，∠ACB＝120°，
P，Q分别为AE，AB的中点。
(1)证明：PQ //平面ACD；
(2)求AD与平面ABE所成角的正弦值。
（（本小题满分12分）
已知点P（x，y）在圆x2+y2－6x－6y+14=0上。
（1）求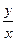
的最大值和最小值；
（2）求x2+y2+2x+3的最大值与最小值；
（本小题满分12分）
如图，是总体的一样本频率分布直方图，且在[15,18）内频数为8。
（1）求样本容量；
（2）若在[12,15）内小矩形面积为0.06，求在[12,15）内的频数；
（3）求样本[18,33]内的频率。
（本小题满分10分）
已知f(x)=2x+a，g(x)=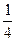
（3+x2），若g[f(x)]=x2+x+1，求a的值。
.(本小题满分12分)
已知函数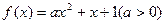
的两个不同的零点为
