四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及 的值;
的值;
(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1, ,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
十一黄金周期间,雁西湖7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 人数变化/万人 |
+0.5 |
+0.7 |
+0.8 |
-0.4 |
-0.6 |
+0.2 |
-0.1 |
(1)请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?
(2)如果9月30日旅游人数为2万人,平均每人消费300元,请问风景区在此7天内总收入为多少万元?
(本题8分)阅读下题解答:
计算: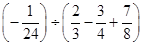 .
.
分析:利用倒数的意义,先求出原式的倒数,再得原式的值.
解: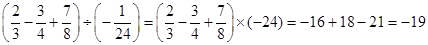 .
.
所以原式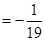 .
.
根据阅读材料提供的方法,完成下面的计算: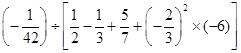
(本题8分)已知a,b互为倒数,c,d互为相反数,并且m的绝对值为1,求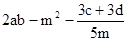
(本题8分)已知: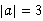 ,
,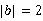 ,且
,且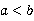 ,求
,求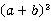 的值.
的值.
(本题6分)在数轴上把下列各数表示出来,并用“<”连接各数.
2,﹣|﹣1|,1 ,0,﹣(﹣3.5)
,0,﹣(﹣3.5)