(本题8分)已知: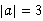 ,
,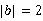 ,且
,且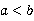 ,求
,求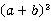 的值.
的值.
某校为了增强学生的疫情防控意识,组织全校2000名学生进行了疫情防控知识竞赛.从中随机抽取了 名学生的竞赛成绩(满分100分),分成四组: ; ; ; ,并绘制出不完整的统计图:
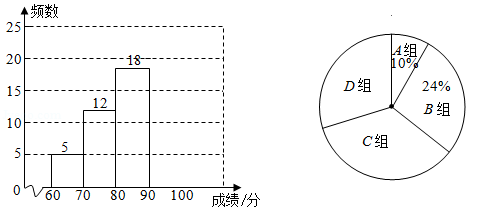
(1)填空: ;
(2)补全频数分布直方图;
(3)抽取的这 名学生成绩的中位数落在 组;
(4)若规定学生成绩 为优秀,估算全校成绩达到优秀的人数.
如图,在矩形 中,点 在边 上,点 在 的延长线上,且 .
求证:(1) ;
(2)四边形 是平行四边形.

先化简,再求值: ,其中 .
计算: .
已知抛物线 , 为常数, 经过点 ,顶点为 .
(Ⅰ)当 时,求该抛物线的顶点坐标;
(Ⅱ)当 时,点 ,若 ,求该抛物线的解析式;
(Ⅲ)当 时,点 ,过点 作直线 平行于 轴, 是 轴上的动点, 是直线 上的动点.当 为何值时, 的最小值为 ,并求此时点 , 的坐标.