一个不透明的布袋里装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球1个，蓝球2个，黄球若干个，现从中任意摸出一个球是蓝球的概率为
．
（1）求口袋中黄球的个数；
（2）甲同学先随机摸出一个小球（不放回），再随机摸出一个小球，请用“树状图法”或“列表法”，求两次摸出都是蓝球的概率；
如图两条相交的直线OX、OY，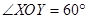
，在射线OX、OY上分别再任意取A、B两点，作∠ABY的平分线BD，BD的反向延长线交
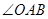的平分线于点C，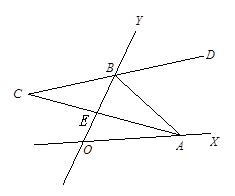
若∠BAX=130°，求∠C的度数？
随着点A、B位置的变化，∠C的大小是否会变化？若保持不变，请求出∠C的度数。
在五边形ABCDE中，∠A=135°，AE⊥ED，AB∥CD，∠B=∠D，试求∠C的度数.
如图，已知∠BAP+∠APD=180°，∠1=∠2.试说明：∠E=∠F.
如图，在△AOB中，A、B两点的坐标分别为（2，4）和（6，2），求△AOB的面积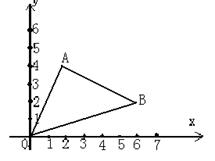
补全下面的说理过程，并在括号内填上适当的理由.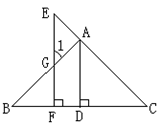
如图所示，AD⊥BC，EF⊥BC，
所以 ∠ADB=∠EFB=90°
所以 EF∥____（）
所以 = ∠1（）
∠CAD = ∠E
因为∠1=∠E，
所以∠=∠CAD（）
所以AD平分∠BAC.