如图，直线
与x轴，y轴分别相交于点B，点C，经过B、C两点的抛物线
与x轴的另一交点为A，顶点为P，且对称轴是直线
．
（1）求A点的坐标及该抛物线的函数表达式；
（2）求出∆PBC的面积；
（3）请问在对称轴右侧的抛物线上是否存在点Q，使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的
？若存在，请求出点Q的坐标；若不存在，请说明理由．
如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，请画出这个几何体的主视图和左视图.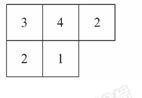
有这样一道题，“当
时，求多项式
的值”，马小虎做题时把
错抄成
，王小真没抄错题，但他们做出的结果却都一样，你知道这是怎么回事吗？说明理由．
某学生由于看错了运算符号，把一个整式减去多项式ab-2bc+3ac误认为是加上这个多项式，结果得出的答案是2bc-3ac+2ab，求原题的正确答案.
在拖拉机油箱中，盛满56千克油，拖拉机工作时，每小时平均耗油6千克，求邮箱里剩下Q（千克）与拖拉机的工作时间t（小时）之间的函数关系式.
解方程：（6+6+6+6=24分）
（1）（y+1）-2(y-1)=1-3y (2)
（3）
(x－3)－
(2x+1)＝1（4）