如图所示,虚线左侧存在非匀强电场,MO是电场中的某条电场线,方向水平向右,长直光滑绝缘细杆CD沿该电场线放置。质量为m1、电量为+q1的A球和质量为m2、电量为+q2的B球穿过细杆(均可视为点电荷)。当t=0时A在O点获得向左的初速度v0,同时B在O点右侧某处获得向左的初速度v1,且v1>v0。结果发现,在B向O点靠近过程中,A始终向左做匀速运动。当t=t0时B到达O点(未进入非匀强电场区域),A运动到P点(图中未画出),此时两球间距离最小。静电力常量为k。
(1)求0~t0时间内A对B球做的功;
(2)求杆所在直线上场强的最大值;
(3)某同学计算出0~t0时间内A对B球做的功W1后,用下列方法计算非匀强电场PO两点间电势差:
设0~t0时间内B对A球做的功为W2,非匀强电场对A球做的功为W3,
根据动能定理 W2+W3=0
又因为 W2=−W1
PO两点间电势差 
请分析上述解法是否正确,并说明理由。
如图为某种鱼饵自动投放器中的投饵管装置示意图,其下半部AB是一长为2R的竖直细管,上半部BC是半径为R的四分之一圆弧弯管,管口沿水平方向,AB管内有一原长为R.下端固定的轻质弹簧。投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上端放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去。设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零。不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能。已知重力加速度为g。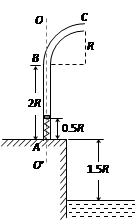
求:
⑴质量为m的鱼饵到达管口C时的速度大小v1;
⑵弹簧压缩到0.5R时的弹性势能Ep;
⑶已知地面与水面相距1.5R,若使该投饵管绕AB管的中轴线OO′在90º角的范围内来回缓慢转动,每次弹射时只放置一粒鱼饵,鱼饵的质量在2m/3到m之间变化,且均能落到水面。持续投放足够长时间后,鱼饵能够落到水面的最大面积S是多少?
以初速为v0,射程(水平距离)为s的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体的速率为多大?其水平方向的速度大小为多少?
车在水平专用测试道上进行测试,该车总质量为m=1×103 kg,由静止开始沿水平测试道运动.传感设备记录其运动的速度时间图象(v-t图象)如图所示.该车运动中受到的摩擦阻力(含空气阻力)恒定,且摩擦力与车对路面压力的比值为μ=0.2.赛车在0~5 s的v-t图线为直线,5 s末达到该车发动机的额定牵引功率并保持该功率行驶,在5 s~50 s之间,赛车的v-t图线是一段曲线,50 s以后为直线.g取10 m/s2,
求:(1)该车发动机牵引力的额定功率P.
(2)该车行驶中的最大速度vm.
(3)该车出发后,前50 s内的位移x.
如图所示,滑雪运动员从一斜坡上的A处,从静止开始下滑到水平平台上的B处,然后继续向前滑行直至离开水平平台,最后落在水平地面上。已知h1 = 60m,h2=20m,滑雪运动员的质量为m=60kg,忽略一切摩擦和空气阻力,g取10m/s2。
求:(1)以水平平台为参考面,运动员开始下滑时的重力势能;
(2)运动员滑到斜坡底端B处时的速度大小;
(3)运动员离开平台后,在水平方向运动的距离。
一辆质量为0.40kg的遥控玩具车,从静止开始出发在平直轨道上行驶。已知发动机的牵引力为0.16N,玩具车在运动过程中受到的阻力为0.12N。求:
(1)玩具车在加速运动过程中的加速度大小
(2)玩具车开始加速运动6.0s内发生的位移