给定数列
(1)判断 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;
(2)是否存在常数 .使
.使 对
对 都成立? 若存在,找出
都成立? 若存在,找出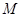 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由.
设函数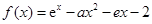 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ) 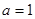 时,求曲线
时,求曲线 在点
在点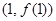 处的切线方程;
处的切线方程;
(Ⅱ)函数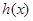 是
是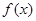 的导函数,求函数
的导函数,求函数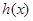 在区间
在区间 上的最小值.
上的最小值.
设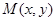 到定点
到定点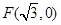 的距离和它到直线
的距离和它到直线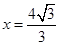 距离的比是
距离的比是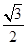 .
.
(Ⅰ)求点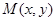 的轨迹方程;
的轨迹方程;
(Ⅱ)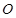 为坐标原点,斜率为
为坐标原点,斜率为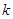 的直线过
的直线过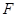 点,且与点
点,且与点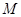 的轨迹交于点
的轨迹交于点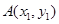 ,
,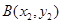 ,若
,若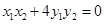 ,求△
,求△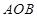 的面积.
的面积.
在梯形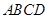 中,
中, ,
, ,
,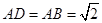 ,
,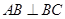 ,如图把
,如图把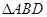 沿
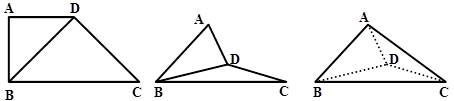
沿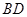 翻折,使得平面
翻折,使得平面 平面
平面 .
.
(Ⅰ)求证: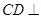 平面
平面 ;
;
(Ⅱ)若点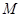 为线段
为线段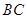 中点,求点
中点,求点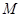 到平面
到平面 的距离.
的距离.
已知某校 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求 社团中各有1名学生的概率.
社团中各有1名学生的概率.
已知 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足 ,
, ,数列
,数列 的前
的前 项和为
项和为
 .
.
(Ⅰ)求数列 的通项公式;(Ⅱ)证明数列
的通项公式;(Ⅱ)证明数列 是等比数列.
是等比数列.