设 是椭圆
是椭圆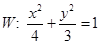 上不关于坐标轴对称的两个点,直线
上不关于坐标轴对称的两个点,直线 交
交 轴于点
轴于点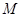 (与点
(与点 不重合),O为坐标原点.
不重合),O为坐标原点.
(1)如果点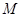 是椭圆
是椭圆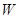 的右焦点,线段
的右焦点,线段 的中点在y轴上,求直线AB的方程;
的中点在y轴上,求直线AB的方程;
(2)设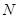 为
为 轴上一点,且
轴上一点,且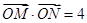 ,直线
,直线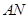 与椭圆
与椭圆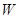 的另外一个交点为C,证明:点
的另外一个交点为C,证明:点 与点
与点 关于
关于 轴对称.
轴对称.
设命题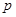 :实数
:实数 满足
满足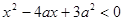 ,其中
,其中 ;命题
;命题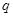 :实数
:实数 满足
满足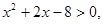 且
且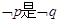 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
已知圆心为 的圆经过点
的圆经过点 .
.
(1)求圆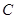 的标准方程;
的标准方程;
(2)若直线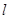 过点
过点 且被圆
且被圆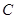 截得的线段长为
截得的线段长为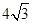 ,求直线
,求直线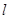 的方程;
的方程;
(3)是否存在斜率是1的直线 ,使得以
,使得以 被圆
被圆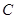 所截得的弦EF为直径的圆经过
所截得的弦EF为直径的圆经过
原点?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
如图,在四棱锥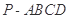 中,
中,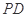 ⊥底面
⊥底面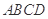 ,底面
,底面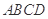
为正方形, ,
, ,
,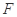 分别是
分别是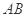 ,
,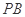 的 中点.
的 中点.
(1)求证: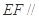 平面
平面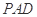 ;
;
(2)求证: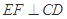 ;
;
(3)若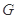 是线段
是线段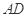 上一动点,试确定
上一动点,试确定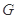 点位置,
点位置,
使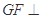 平面
平面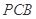 ,并证明你的结论.
,并证明你的结论.
在△ABC中,已知c=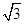 ,b=1,B=30°.(1)求角A; (2)求△ABC的面积.
,b=1,B=30°.(1)求角A; (2)求△ABC的面积.
已知圆心为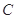 的圆经过点
的圆经过点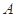 (0,
(0,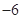 ),
),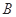 (1,
(1,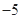 ),且圆心在直线
),且圆心在直线 :
: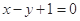 上,求圆心为
上,求圆心为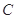 的圆的标准方程.
的圆的标准方程.