已知直线y=﹣x+1与椭圆 +
+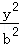 =1(a>b>0)相交于A、B两点.
=1(a>b>0)相交于A、B两点.
①若椭圆的离心率为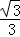 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
②若向量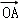 与向量
与向量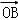 互相垂直(其中O为坐标原点),当椭圆的离心率e∈[
互相垂直(其中O为坐标原点),当椭圆的离心率e∈[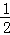 ,
,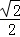 ]时,求椭圆的长轴长的最大值.
]时,求椭圆的长轴长的最大值.
已知数列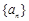 的前n项和
的前n项和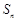 满足:
满足: (a为常数,且
(a为常数,且 ).
).
(Ⅰ)求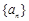 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设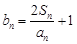 ,若数列
,若数列 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设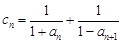 ,数列
,数列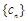 的前n项和为Tn .
的前n项和为Tn .
求证: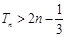 .
.
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 ,最小值为
,最小值为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线 与椭圆
与椭圆 相交于
相交于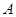 ,
, 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以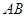 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N) 顺次为一次函数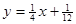 图象上的点, 点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N) 顺次为x轴正半轴上的点,其中x1=a(0<a<1), 对于任意n∈N,点An、Bn、An+1构成以 Bn为顶点的等腰三角形.
图象上的点, 点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N) 顺次为x轴正半轴上的点,其中x1=a(0<a<1), 对于任意n∈N,点An、Bn、An+1构成以 Bn为顶点的等腰三角形.
⑴求{yn}的通项公式,且证明{yn}是等差数列;
⑵试判断xn+2-xn是否为同一常数(不必证明),并求出数列{xn}的通项公式;
⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;若不存在, 请说明理由.
、已知二次函数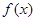 满足:①在x=1时有极值;②图像过点
满足:①在x=1时有极值;②图像过点 ,且在该点处的切线与直线
,且在该点处的切线与直线 平行.
平行.
(1)求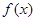 的解析式;
的解析式;
(2)求函数 的值域;
的值域;
(3)若曲线 上任意两点的连线的斜率恒大于
上任意两点的连线的斜率恒大于 ,求
,求 的取值范围.
的取值范围.
、已知向量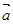 ="(1,2),"
="(1,2)," 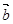 =(-2,1),k,t为正实数,向量
=(-2,1),k,t为正实数,向量  =
= 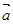 +(t
+(t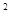 +1)
+1)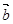 ,
,  =-k
=-k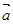 +
+
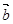
(1)若 ⊥
⊥ ,求k的最小值;
,求k的最小值;
(2)是否存在正实数k、t,使 ∥
∥ ?若存在,求出k的取值范围;若不存在,请说明理由.
?若存在,求出k的取值范围;若不存在,请说明理由.