各项均不为零的数列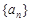 的前
的前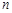 项和为
项和为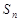 ,且
,且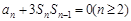 ,
,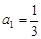 .
.
(1)求数列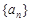 的通项公式
的通项公式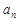 ;
;
(2)若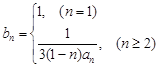 ,设
,设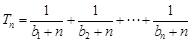 ,若
,若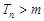 对
对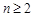 恒成立,求实数
恒成立,求实数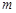 的取值范围.
的取值范围.
观察下列等式 第一个式子
第一个式子 第二个式子
第二个式子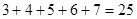 第三个式子
第三个式子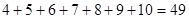 第四个式子
第四个式子
照此规律下去
(Ⅰ)写出第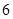 个等式;
个等式;
(Ⅱ)你能做出什么一般性的猜想?请用数学归纳法证明猜想.
用0,1,2,3,4这五个数字组成无重复数字的自然数。
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数。
设递增数列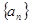 满足
满足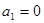 ,
,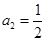 且
且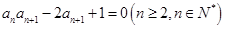 .
.
(1)证明:数列 是等差数列;
是等差数列;
(2)设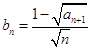 ,记数列
,记数列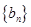 的前
的前 项和为
项和为 ,使得不等式
,使得不等式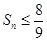 成立的最大正整数
成立的最大正整数 的值.
的值.
已知函数 为奇函数。
为奇函数。
(1)求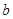 的值;
的值;
(2)证明:函数 在区间(1,
在区间(1, )上是减函数;
)上是减函数;
(3)解关于x的不等式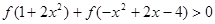 .
.
复数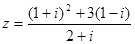 ,若
,若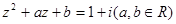 ,求
,求 的值.
的值.