某中学在运动会期间举行定点投篮比赛,规定每人投篮4次,投中一球得2分,没有投中得0分,假设每次投篮投中与否是相互独立的,已知小明每次投篮投中的概率都是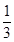 .
.
(1)求小明在投篮过程中直到第三次才投中的概率;
(2)求小明在4次投篮后的总得分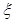 的分布列和期望.
的分布列和期望.
已知椭圆 (
( )过点
)过点 (0,2),离心率
(0,2),离心率 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点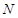 (2,0)的直线
(2,0)的直线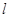 与椭圆相交于
与椭圆相交于 两点,且
两点,且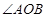 为锐角(其中
为锐角(其中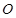 为坐标原点),求直线
为坐标原点),求直线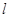 倾斜角的取值范围.
倾斜角的取值范围.
已知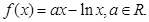
(Ⅰ)当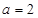 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若 在
在 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(Ⅲ)是否存在实数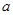 ,使
,使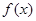 在区间
在区间 的最小值是3,若存在,求出
的最小值是3,若存在,求出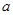 的值;
的值;
若不存在,说明理由.
如图,矩形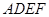 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,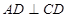 ,
,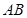 ∥
∥ ,
, ,
, ,
,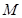 为
为 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面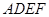 ;
;
(Ⅱ)求证:平面
 平面
平面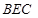 ;
;
(Ⅲ)若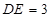 ,求平面
,求平面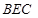 与平面
与平面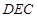 所成锐二面角的余弦值.
所成锐二面角的余弦值.
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
| 甲 |
乙 |
|
| 1 |
8 |
|
| 6 0 0 |
2 |
4 4 |
| 2 |
3 |
0 |
(Ⅰ)求乙球员得分的平均数和方差;
(Ⅱ)分别从两人得分中随机选取一场的得分,求得分和Y的分布列和数学期望.
(注:方差
其中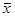 为
为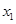 ,
,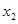 ,
,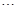
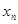 的平均数)
的平均数)
已知函数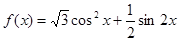 .
.
(Ⅰ)求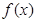 的最小正周期;
的最小正周期;
(Ⅱ)求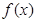 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.