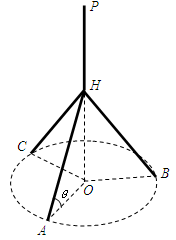
如图所示,某人想制造一个支架,它由四根金属杆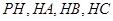 构成,其底端三点
构成,其底端三点 均匀地固定在半径为
均匀地固定在半径为 的圆
的圆 上(圆
上(圆 在地面上),
在地面上), 三点相异且共线,
三点相异且共线,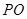 与地面垂直. 现要求点
与地面垂直. 现要求点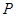 到地面的距离恰为
到地面的距离恰为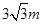 ,记用料总长为
,记用料总长为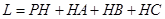 ,设
,设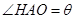 .
.
(1)试将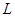 表示为
表示为 的函数,并注明定义域;
的函数,并注明定义域;
(2)当 的正弦值是多少时,用料最省?
的正弦值是多少时,用料最省?
(本小题满分13分)已知数列{an}的前n项和为Sn,又a1=1,a2=2,且满足Sn+1=kSn+1,
(1)求k的值及{an}的通项公式;
(2)若 ,求证:
,求证: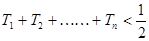 .
.
(本小题满分10分)设△ABC的内角A、B、C的对边长分别为a、b、c,设S为△ABC的面积,
满足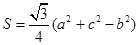 .
.
(Ⅰ)求B;
(Ⅱ)若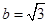 ,设
,设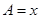 ,
,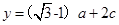 ,求函数
,求函数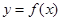 的解析式和最大值.
的解析式和最大值.
如图,直线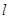 过点
过点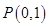 ,夹在两已知直线
,夹在两已知直线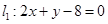 和
和 之间的线段
之间的线段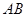 恰被点
恰被点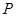 平分.
平分.
(Ⅰ)求直线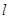 的方程;
的方程;
(Ⅱ)设点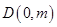 ,且
,且 ,求:
,求: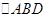 的面积.
的面积.
(本小题满分13分)已知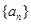 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足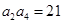 ,
,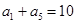 ,数列
,数列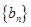 满足
满足 .
.
(Ⅰ)求数列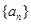 的通项公式;
的通项公式;
(Ⅱ)求数列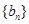 的前
的前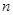 项和
项和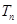 .
.
(本小题满分13分)在 中,已知
中,已知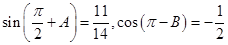 .
.
(Ⅰ)求sinA与角B的值;
(Ⅱ)若角A,B,C的对边分别为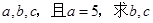 的值.[
的值.[