(本小题满分10分)设△ABC的内角A、B、C的对边长分别为a、b、c,设S为△ABC的面积,
满足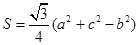 .
.
(Ⅰ)求B;
(Ⅱ)若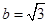 ,设
,设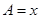 ,
,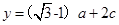 ,求函数
,求函数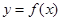 的解析式和最大值.
的解析式和最大值.
写出图⑴的程序框图的运行结果是多少.
 |
设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以x表示显性基因,y表示隐性基因,则具有xx基因的人为纯显性,具有yy基因的人是纯隐性。纯显性与混合性的人都有显露显性基因决定的某一特征,孩子从父母身上各得到1个基因。假定父母都是混合性,问:
(1)1个孩子由显性基因决定的特征的概率是多少?
(2)2个孩子中至少有一个显性基因决定的特征的概率是多少?
加工某种零件需经过三道工序,设第一、二、三道工序的合格率分别为 、
、 、
、 ,且各道工序互不影响。
,且各道工序互不影响。
(1)求该种零件的合格率;
(2)从该种零件中任取三件,求恰好取到一件合格品的概率和至少取到一件合格品的概率。
已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支。求:
(1)A、B两组中有一组恰有两支弱队的概率;
(2)A组中至少有两支弱队的概率。
从一副扑克牌(没有大、小王)的52张牌中任取两张,求:
(1)两张是不同花色牌的概率;
(2)至少有一张是红心的概率.