如图，矩形ABCD中，|AB|＝4，|BC|＝2，E，F，M，N分别是矩形四条边的中点，G，H分别是线段ON，CN的中点．
（1）证明：直线EG与FH的交点L在椭圆W：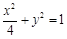
上；
（2）设直线l：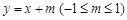
与椭圆W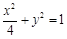：有两个不同的交点P，Q，直线l与矩形ABCD有两个不同的交点S，T，求
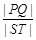的最大值及取得最大值时m的值．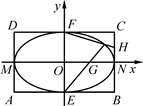
设函数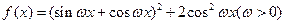
的最小正周期为
．
（Ⅰ）求
的最小正值．
（Ⅱ）若函数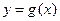
的图像是由
的图像向右平移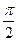
个单位长度得到，求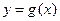的单调增区间
一艘缉私巡逻艇在小岛A南偏西
方向，距小岛3海里的B处，发现隐藏在小岛边上的一艘走私船正开始向岛北偏西
方向行驶，测得其速度为10海里/小时，问巡逻艇需用多大的速度朝什么方向行驶，恰好用0.5小时在C处截住该走私船？
（参考数据：
）
已知向量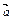
＝(sin
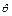，1)，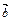
＝(1，cos)，－
．
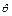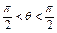(1) 若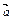⊥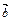，求；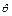
(2) 求|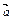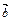＋|的最大值．
设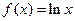
，
．
（1）求
的单调区间和最小值；
（2）讨论与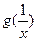
的大小关系；
（3）求
的取值范围，使得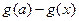
＜
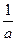对任意
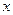＞0成立
为了保护环境，发展低碳经济，某
单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本
（元）与月处理量
（吨）之间的函数关系可近似的表示为：
，且每处理一吨二氧化碳得到可利用的化工产品
价值为100元．
（1）该单位每月处理量为多少吨时，才能使每吨的平均处理
成本最低？
（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴
多少元才能使该单位不亏损？