如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直于AB于F,连接AE,BE,证明:
(1)∠FEB=∠CEB;
(2)EF2=AD•BC.
设一部机器在一天内发生故障的概率为0 2,机器发生故障时全天停止工作
2,机器发生故障时全天停止工作 若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?
若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?
设P在[0,5]上随机地取值,求方程x2+px+ =0有实根的概率.
=0有实根的概率.
已知连续型随机变量ζ的概率密度函数f(x)=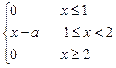
(1)求常数a的值,并画出ζ的概率密度曲线;
(2)求P(1<ζ<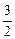 )
)
甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,计算:
(1)两人都击中目标的概率;
(2)其中恰有一人击中目标的概率;
(3)至少有一人击中目标的概率.
如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作, 已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90,分别求系统N1,N2正常工作的概率P1、P2.