如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺时针旋转得到△AB′D′.
①当旋转角为 度时,边AD′落在AE上;
②在①的条件下,延长DD’交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.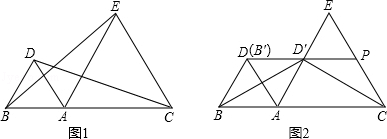
随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
为加快城乡对接,建设全域美丽乡村,某地区对 、 两地间的公路进行改建.如图, 、 两地之间有一座山,汽车原来从 地到 地需途经 地沿折线 行驶,现开通隧道后,汽车可直接沿直线 行驶.已知 千米, , .
(1)开通隧道前,汽车从 地到 地大约要走多少千米?
(2)开通隧道后,汽车从 地到 地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ,

为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)
请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?

如图,已知二次函数 , 为实数)的图象过点 ,一次函数 , , 为实数)的图象 经过点 .
(1)求 值并写出二次函数表达式;
(2)求 值;
(3)设直线 与二次函数图象交于 , 两点,过 作 垂直 轴于点 ,试证明: ;
(4)在(3)的条件下,请判断以线段 为直径的圆与 轴的位置关系,并说明理由.

2017年9月8日 日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的 点出发 米),沿俯角为 的方向直线飞行1400米到达 点,然后打开降落伞沿俯角为 的方向降落到地面上的 点,求该选手飞行的水平距离 .
