如图,在直三棱柱 中,平面
中,平面 侧面
侧面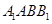 ,且
,且
(1) 求证: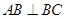 ;
;
(2) 若直线 与平面
与平面 所成的角为
所成的角为 ,求锐二面角
,求锐二面角 的大小。
的大小。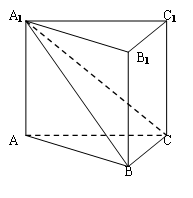
(本小题满分12分)已知:正项数列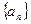 的前
的前 项和为
项和为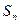 ,方程
,方程 有一根为
有一根为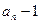
(1)求数列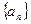 的通项
的通项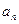 .
.
(2)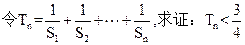 .
.
(本小题满分12分)已知向量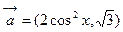 ,
,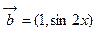 ,函数
,函数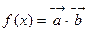 ,
,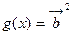 .
.
(1)求函数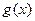 的最小正周期;
的最小正周期;
(2)在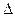
 中,
中,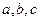 分别是角
分别是角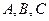 的对边,且
的对边,且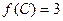 ,
,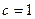 ,
,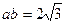 ,且
,且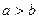 ,求
,求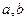 的值.
的值.
、(本小题满分14分)已知点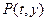 在函数
在函数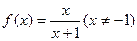 的图象上,且有
的图象上,且有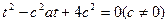 .
.
(1) 求证: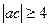 ;
;
(2) 求证:在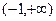 上
上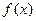 单调递增.
单调递增.
(3) 求证: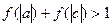 .
.
(本小题满分12分)已知两定点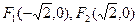 满足条件
满足条件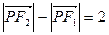 的点P的轨迹是曲线E,直线
的点P的轨迹是曲线E,直线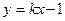 与曲线E交于A、B两点。
与曲线E交于A、B两点。
(1)求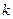 的取值范围;
的取值范围;
(2)如果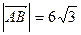 且曲线E上存在点C,使
且曲线E上存在点C,使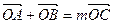 ,求
,求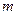 的值及点C的坐标.
的值及点C的坐标.
(本小题满分14分)已知双曲线 的左、右顶点分别为
的左、右顶点分别为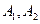 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线 与
与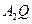 交点的轨迹E的方程
交点的轨迹E的方程
(2若过点 的两条直线
的两条直线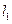 和
和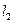 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且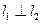 ,求
,求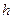 的值.
的值.