已知数列 中,
中,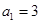 ,前
,前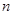 项和
项和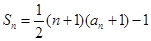 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设数列 的前
的前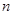 项和为
项和为 ,是否存在实数
,是否存在实数 ,使得
,使得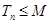 对一切正整数
对一切正整数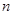 都
都
成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
已知椭圆C的中心在原点,左焦点为F1,其右焦点F2和右准线分别是抛物线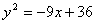 的顶点和准线.
的顶点和准线.
⑴求椭圆C的方程;
⑵若点P为椭圆上C的点,△PF1F2的内切圆的半径为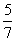 ,求点P到x轴的距离;
,求点P到x轴的距离;
⑶若点P为椭圆C上的一个动点,当∠F1PF2为钝角时求点P的取值范围.
已知双曲线的方程为 , 直线
, 直线 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知: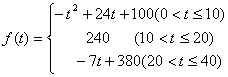
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
某厂在计划期内要安排生产甲、乙两种产品,这些产品分别需要在A、B、C、D四种不同的设备上加工,按工艺规定,产品甲和产品乙在各设备上需要的加工台时数于下表给出.已知各设备在计划期内有效台时数分别是12,8,16,12(一台设备工作一小时称为一台时),该厂每生产一件产品甲可得利润2元,每生产一件产品乙可得利润3元,问应如何安排生产计划,才能获得最大利润?
| 设备 产品 |
A |
B |
C |
D |
| 甲 |
2 |
1 |
4 |
0 |
| 乙 |
2 |
2 |
0 |
4 |
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线 上,
上, 与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)