某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天．
（1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？
（2）若学校每天需付给甲队的绿化费用为0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？
（1）先化简，再求值：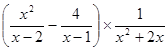 
，其中
；
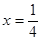（2）解不等式组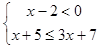
，并写出它的整数解.
如图，是
的正方形网格，⊿ABC是格点三角形（顶点在小正方形顶点上）.
（1）求△ABC的面积；
（2）请画出与⊿ABC相似但不全等的另一个格点三角形，并写出与原三角形的相似比与面积比.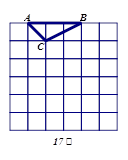
给出三个多项式：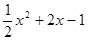
，
，
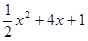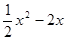，请选择你喜欢的两个多项式进行加法运算，并把结果分解因式。
已知：在矩形AOBC中，OB＝4，OA＝3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点（不与B、C重合），过F点的反比例函数
（k＞0）的图象与AC边交于点E.
（1）求证：△AOE与△BOF的面积相等.
（2）记S＝S△OEF－S△ECF，求当k为何值时，S有最大值，最大值为多少？
（3）请探索：是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存在，请直接写出点F的坐标，若不存在，请说明理由.
将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB＝2
，P是线段AC上的一个动点．
（1）当点P运动到∠ABC的平分线上时，连结DP，求DP的长；
（2）当点P在运动过程中出现PD＝BC时，∠PDA=；
（3）当PC=时，以D，P，B，Q为顶点的平行四边形的顶点Q恰好在边BC上，此时□DPBQ的面积=．