甲、乙两名同学进入初四后,某科6次考试成绩如图:
(1)请根据下图填写如表:
| |
平均数 |
方差 |
中位数 |
众数 |
极差 |
| 甲 |
75 |
|
75 |
|
|
| 乙 |
|
33.3 |
|
|
15 |
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:
①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?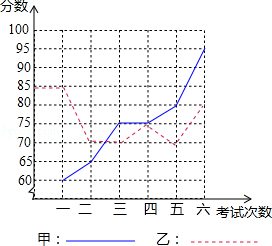
补全证明过程
已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。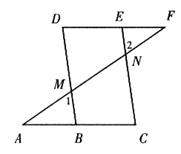
证明:∵∠1=∠2(已知),
又∠1=∠DMN(___________________),
∴∠2=∠_________(等量代换)。
∴DB∥EC(同位角相等,两直线平行)。
∴∠A=∠F(两直线平行,内错角相等)。
已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
| △ABC |
A(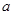 ,0) ,0) |
B(3,0) |
C(5,5) |
| △A′B′C′ |
A′(4,2) |
B′(7,b) |
C′(c,7) |
(1)观察表中各对应点坐标的变化,并填空: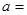 __________,
__________,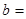 __________,
__________,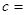 __________;
__________;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′
(3)直接写出△A′B′C′的面积是__________。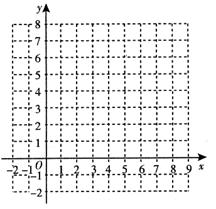
已知:关于x,y的方程组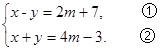 的解为负数,求m的取值范围.
的解为负数,求m的取值范围.
(1)解不等式3(x+1)<4(x-2)-3,并把它的解集表示在数轴上;
(2).求不等式组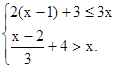 的整数解.
的整数解.
如图,抛物线 与
与 轴的交点为A、B,与
轴的交点为A、B,与 轴的交点为C,顶点为
轴的交点为C,顶点为 ,将抛物线
,将抛物线 绕点B旋转
绕点B旋转 ,得到新的抛物线
,得到新的抛物线 ,它的顶点为D.
,它的顶点为D.
(1)求抛物线 的解析式;
的解析式;
(2)设抛物线 与
与 轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为
轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围;
的取值范围;
(3)设抛物线 的对称轴与
的对称轴与 轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.