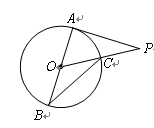
如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据: ≈1.41,
≈1.41, ≈2.45)
≈2.45)
小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图像如图中的折线段OA-OB所示.
(1)试求折线段OA-OB所对应的函数关系式;
(2)请解释图中线段AB的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离 (千米)与小明出发后的时间
(千米)与小明出发后的时间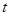 (分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为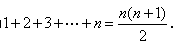
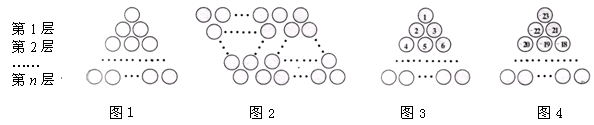
如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,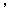
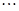 ,则最底层最左边这个圆圈中的数是;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,
,则最底层最左边这个圆圈中的数是;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,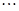 ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和.
某商场搞摸奖促销活动:商场在一只不透明的箱子里放了三个相同的小球,球上分别写有“10元”、“20元”、“30元”的字样.规定:顾客在本商场同一日内,每消费满100元,就可以在这只箱子里摸出一个小球(顾客每次摸出小球看过后仍然放回箱内搅匀),商场根据顾客摸出小球上所标金额就送上一份相应的奖品.现有一顾客在该商场一次性消费了235元,按规定,该顾客可以摸奖两次,求该顾客两次摸奖所获奖品的价格之和超过40元的概率.
如图是甲、乙两人在一次射击比赛中击中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数所在圆环被击中所得的环数)每人射击了6次.
(1)请用列表法将他俩的射击成绩统计出来;
(2)请你用学过的统计知识,对他俩的这次射击情况进行比较.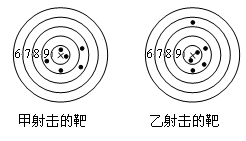
如图,AB是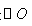
 ,
,