课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).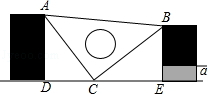
已知:如图,在平面直角坐标系中,点 , ,过点 的直线 与 轴正半轴交于点 ,与直线 交于点 .
(1)当 且 时,求 的长度;
(2)若点 的坐标是 ,且 ,求经过点 且以点 为顶点的抛物线的函数表达式.

如图,在 中, , , , ,点 是边 上一点,连接 ,将 沿 翻折得到 .
(1)若 , ,且 ,求 的长;
(2)连接 ,若四边形 是平行四边形,求 与 之间的关系式.

如图, ,点 为射线 上的一动点.过点 作 于点 .点 在 内,且满足 , .
(1)当 时,求点 到 的距离;
(2)在射线 上是否存在一定点 ,使得 ?若存在,请用直尺(不带刻度)和圆规作出点 (不必写作法,但要保留作图痕迹),并求 的长;若不存在,说明理由.

商场从某厂以75元 件的价格采购一种商品,售价是100元 件.厂家与商场约定:若商场一次性采购达到或超过400件,厂家按每件5元返利给 商场.商场没有售完的,可以以65元 件退还给厂家.设 商场售出该商品 件,问: 商场对这种商品的销量至少要多少时,他们的获利能达到9600元?
如图,在 中, , 是 的角平分线,点 在边 上.过点 、 的圆的圆心 在边 上,它与边 交于另一点 .
(1)试判断 与圆 的位置关系,并说明理由;
(2)若 , ,求 的长.
