其中第(1)(2)问文理科学生都要做,第(3)问按题目要求分文理来做。
已知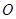 为坐标原点,向量
为坐标原点,向量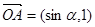 ,
,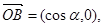
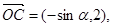 点
点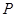 是直线
是直线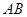 上的一点,且
上的一点,且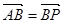 .
.
求点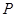 的坐标(用
的坐标(用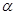 表示);
表示);
若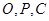 三点共线,求以线段
三点共线,求以线段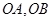 为邻边的平行四边形的对角线长;
为邻边的平行四边形的对角线长;
(3)(文科生做)记函数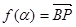 •
•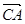 ,且
,且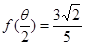 ,求
,求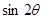 的值.
的值.
(3)(理科生做)记函数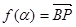 •
•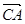 ,
,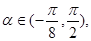 讨论函数
讨论函数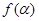 的单调性,并求其值域.
的单调性,并求其值域.
选修4-4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为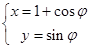 ,(
,(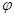 为参数),以
为参数),以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线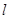 的极坐标方程是
的极坐标方程是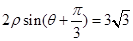 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线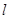 的交点为
的交点为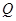 ,求线段
,求线段 的长.
的长.
选修4-1:几何证明选讲
如图,四边形 内接于圆,
内接于圆, ,过
,过 点的圆的切线与
点的圆的切线与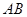 的延长线交于
的延长线交于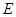 点.
点.
(1)求证: ;
;
(2)若 ,求
,求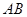 的长.
的长.
设函数 的导函数为
的导函数为 ,且
,且 .
.
(1)求 的解析式;
的解析式;
(2)若方程 在区间
在区间 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数 的取值范围.
的取值范围.
已知椭圆 中,椭圆长轴长是短轴长的
中,椭圆长轴长是短轴长的 倍,短轴的一个端点与两个焦点构成的三角形的面积为
倍,短轴的一个端点与两个焦点构成的三角形的面积为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知动直线 与椭圆
与椭圆 相交于
相交于 两点,
两点,
①若线段 的中点的横坐标为
的中点的横坐标为 ,求斜率
,求斜率 的值;
的值;
②已知点 ,求证:
,求证: 为定值.
为定值.
如图,在几何体 中,
中, 平面
平面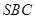 ,
,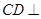 平面
平面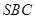 ,
, ,
, ,
, 是线段
是线段 的中点.
的中点.
(1)求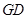 与平面
与平面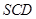 所成角的正弦值;
所成角的正弦值;
(2)求平面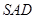 与平面
与平面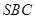 所成锐二面角的余弦值.
所成锐二面角的余弦值.