已知椭圆 中,椭圆长轴长是短轴长的
中,椭圆长轴长是短轴长的 倍,短轴的一个端点与两个焦点构成的三角形的面积为
倍,短轴的一个端点与两个焦点构成的三角形的面积为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知动直线 与椭圆
与椭圆 相交于
相交于 两点,
两点,
①若线段 的中点的横坐标为
的中点的横坐标为 ,求斜率
,求斜率 的值;
的值;
②已知点 ,求证:
,求证: 为定值.
为定值.
命题 方程
方程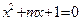 有两个不等的正实数根,命题
有两个不等的正实数根,命题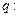 方程
方程 无实数根若“
无实数根若“ 或
或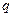 ”为真命题,求
”为真命题,求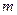 的取值范围
的取值范围
已知下列三个方程: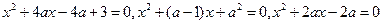 至少有一个方程有实数根,求实数
至少有一个方程有实数根,求实数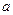 的取值范围
的取值范围
已知函数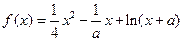 ,其中常数
,其中常数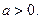
(I)若 处取得极值,求a的值;
处取得极值,求a的值;
(II)求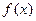 的单调递增区间;
的单调递增区间;
(III)已知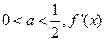 表示
表示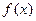 的导数,若
的导数,若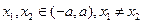 ,
,
且满足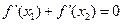 ,试比较
,试比较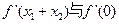 的大小,
的大小, 并加以证明。
并加以证明。
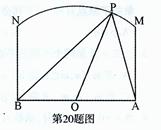
如图,两县城A和B相距20km,O为AB的中点,现要在以O为圆心、20km为半径的圆弧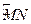 上选择一点P建造垃圾处理厂,其中
上选择一点P建造垃圾处理厂,其中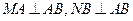 。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9。记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,
。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9。记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,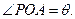
(I)写出x关于 的函数关系,并求该函数的定义域和值域;
的函数关系,并求该函数的定义域和值域;
(II)当x为多少km时,总影响度最小?
如图1,在直角梯形ABCD中,AB//CD,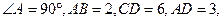 E为CD上一点,且DE=4,过E作EF//AD交BC于F现将
E为CD上一点,且DE=4,过E作EF//AD交BC于F现将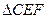 沿EF折到
沿EF折到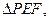 使
使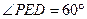 ,如图2。
,如图2。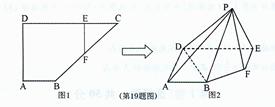
(I)求证:PE⊥平面ADP ;
;
(II)求异面直线BD与PF所成角的余弦值;
(III)在线段PF上是否存在一点M,使DM与平在ADP所成的角为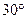 ?若存在,确定点M的位置;若不存在,请说明理由。
?若存在,确定点M的位置;若不存在,请说明理由。