某校从高一年级周末考试的学生中抽出6O名学生,其成绩(均为整数)的频率分布直方图如图所示:(1)依据频率分布直方图,估计这次考试的及格率(60分及以上为及格)和平均分;(2)已知在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,96,97,98,99,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.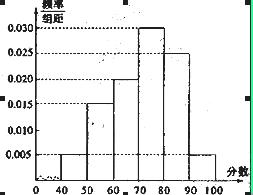
已知数列{an}的前n项和为Sn, 且满足a1 = 2, nan + 1 = Sn + n(n + 1).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列 }的前n项和, 求Tn;
}的前n项和, 求Tn;
(Ⅲ)设 , 证明:
, 证明:
选修4-5: 不等式选讲
已知函数 f (x)=" |x" - 2|,g(x)=" -|x" + 3| +m.
(Ⅰ)若关于x的不等式 g(x)≥0的解集为 [-5, -1], 求实数m的值;
(Ⅱ)若 f (x)的图象恒在 g(x)图象的上方, 求实数m的取值范围.
选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C( ), 半径r =
), 半径r = .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈  , 直线
, 直线 的参数方程为
的参数方程为 为参数), 直线
为参数), 直线 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.
(本小题满分10分)选修4-5:不等式选讲
已知实数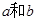
 ,若不等式
,若不等式 有解,记实数M的最小值为m.
有解,记实数M的最小值为m.
(1)求m的值;
(2)解不等式 .
.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系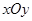 中,直线l的参数方程为
中,直线l的参数方程为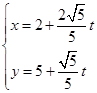 (
( 为参数),若以O为极点,
为参数),若以O为极点, 轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 .
.
(1)求直线l和曲线C的直角坐标方程;
(2)当 时,求直线l与曲线C公共点的极坐标.
时,求直线l与曲线C公共点的极坐标.