在平面直角坐标系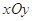
中，已知曲线
: 
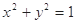，在极坐标系（与平面直角坐标系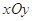取相同的长度单位，且以原点
为极点，以
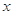轴正半轴为极轴）中，直线
的极坐标方程为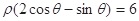
.
（1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的
倍、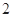
倍后得到曲线
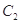，试写出直线的直角坐标方程和曲线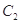的参数方程；
（2）在曲线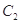上求一点
，使点到直线的距离最大，并求出此最大值.
已知{an}是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn,设集合A={(an,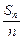
)|n∈N*},B={(x,y)|
x2－y2=1,x,y∈R}.
试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明
(1)若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
(2)A∩B至多有一个元素；
(3)当a1≠0时，一定有A∩B≠
.
已知集合A={(x,y)|x2+mx－y+2=0},B={(x,y)|x－y+1=0,且0≤x≤2},如果A∩B≠
,求实数m的取值范围.
向50名学生调查对A、B两事件的态度，有如下结果: 赞成A的人数是全体的五分之三，其余的不赞成，赞成B的比赞成A的多3人，其余的不赞成；另外，对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人. 问对A、B都赞成的学生和都不赞成的学生各有多少人？
设A={(x,y)|y2－x－1=0},B={(x,y)|4x2+2x－2y+5=0},C={(x,y)|y=kx+b},是否存在k、b∈N,使得(A∪B)∩C=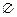
，证明此结论.
设函数
，其中
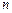为正整数.
（1）判断函数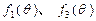
的单调性，并就
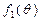的情形证明你的结论；
（2）证明：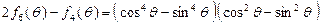
；
（3）对于任意给定的正整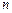数，求函数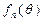
的最大值和最小值.