在甲、乙两个盒子中分别装有标号为1，2，3，4的四个球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等.
（1）求取出的两个球上标号为相邻整数的概率；
（2）求取出的两个球上标号之和能被3整除的概率.
计算：
（1）
; (2)
;
(3)
+
; (4) 
.
函数f(x)=ax3-2bx2+cx+4d (a,b,c,d∈R)的图象关于原点对称，且x=1时，f(x)取极小值为-
.
（1）求a,b,c,d的值；
（2）证明：当x∈［-1，1］时，图象上不存在两点使得过此两点处的切线互相垂直；
（3）若x1,x2∈［-1，1］时，求证：|f(x1)-f(x2)|≤
.
函数y=
,写出求该函数值的算法及流程图.
设f（x）=ax2+bx+c（a≠0)，若函数f(x+1)与f(x)的图象关于y轴对称.求证：f(x+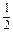
)为偶函数.
已知复数z=a+bi(a,b∈R)且a2+b2=25,(3+4i)z是纯虚数，求z的共轭复数.