已知命题p:|x2-x|≥6,q:x∈Z,且“p且q”与“非q”同时为假命题,求x的值.
写出下列命题的“非P”命题,并判断其真假:
(1)若 有实数根.
有实数根.
(2)平方和为0的两个实数都为0.
(3)若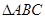 是锐角三角形, 则
是锐角三角形, 则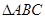 的任何一个内角是锐角.
的任何一个内角是锐角.
(4)若 ,则
,则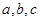 中至少有一为0.
中至少有一为0.
(5)若 ,则
,则
若三条抛物线 中至少有一条与x轴有公共点,求a的取值范围.
中至少有一条与x轴有公共点,求a的取值范围.
写出下列命题的“非P”命题,并判断其真假:
(1)若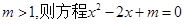 有实数根.
有实数根.
(2)平方和为0的两个实数都为0.
(3)若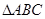 是锐角三角形, 则
是锐角三角形, 则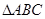 的任何一个内角是锐角.
的任何一个内角是锐角.
(4)若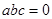 ,则
,则 中至少有一为0.
中至少有一为0.
(5)若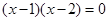 ,则
,则 .
.
已知命题p:方程 有两个不等的负实根, 命题q:方程
有两个不等的负实根, 命题q:方程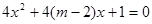 无实根.若p或q为真,p且q为假,求实数m的取值范围.
无实根.若p或q为真,p且q为假,求实数m的取值范围.