(本小题共13分)已知椭圆 的左焦点为
的左焦点为 ,过点M(-3,0)作一条斜率大于0的直线
,过点M(-3,0)作一条斜率大于0的直线 与W交于不同的两点A、B,延长BF交W于点C.
与W交于不同的两点A、B,延长BF交W于点C.
(1)求椭圆W的离心率;
(2)求证:点A与点C关于 轴对称.
轴对称.
已知椭圆 :
: 的左、右顶点分别为
的左、右顶点分别为 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 ,离心率是
,离心率是 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若点 是椭圆
是椭圆 上异于
上异于 ,
, 的任意一点,直线
的任意一点,直线 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 (
( 为椭圆
为椭圆 的右焦点).
的右焦点).
已知函数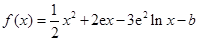 在
在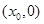 处的切线斜率为零.
处的切线斜率为零.
(Ⅰ)求 和
和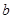 的值;
的值;
(Ⅱ)求证:在定义域内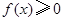 恒成立;
恒成立;
(Ⅲ) 若函数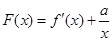 有最小值
有最小值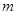 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
如图1,在边长为 的正三角形
的正三角形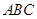 中,
中, ,
,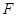 ,
, 分别为
分别为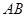 ,
,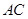 ,
,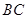 上的点,且满足
上的点,且满足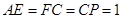 .将△
.将△ 沿
沿 折起到△
折起到△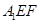 的位置,使二面角
的位置,使二面角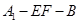 成直二面角,连结
成直二面角,连结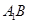 ,
,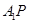 .(如图2)
.(如图2)
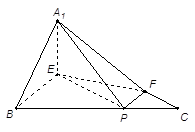
(Ⅰ)求证: ⊥平面
⊥平面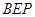 ;
;
(Ⅱ)求直线 与平面
与平面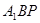 所成角的大小.
所成角的大小.
某工厂生产甲、乙两种产品,甲产品的一等品率为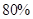 ,二等品率为
,二等品率为 ;乙产品的一等品率为
;乙产品的一等品率为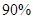 ,二等品率为
,二等品率为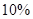 .生产
.生产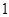 件甲产品,若是一等品,则获利
件甲产品,若是一等品,则获利 万元,若是二等品,则亏损
万元,若是二等品,则亏损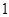 万元;生产
万元;生产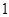 件乙产品,若是一等品,则获利
件乙产品,若是一等品,则获利 万元,若是二等品,则亏损
万元,若是二等品,则亏损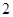 万
万
元.两种产品生产的质量相互独立.
(Ⅰ)设生产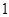 件甲产品和
件甲产品和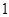 件乙产品可获得的总利润为
件乙产品可获得的总利润为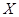 (单位:万元),求
(单位:万元),求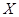 的分布列;
的分布列;
(Ⅱ)求生产 件甲产品所获得的利润不少于
件甲产品所获得的利润不少于 万元的概率.
万元的概率.
已知函数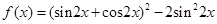 .
.
(Ⅰ)求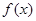 的最小正周期;
的最小正周期;
(Ⅱ)若函数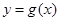 的图象是由
的图象是由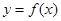 的图象向右平移
的图象向右平移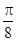 个单位长度,再向上平移1个单位长度得到的,当
个单位长度,再向上平移1个单位长度得到的,当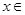 [
[ ,
, ]时,求
]时,求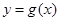 的最大值和最小值.
的最大值和最小值.