丹东市对教师试卷讲评课中学生参与的深度和广度进行评价，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制了如图两幅不完整的统计图，请根据图中所给信息解答下列问题：
（1）在这次评价中，一共抽查了 _________ 名学生；
（2）请将条形统计图补充完整；
（3）如果全市有16万名初中学生，那么在试卷讲评课中，“独立思考”的学生约有多少万人？
如图，已知⊙Ｏ的弦ＡＢ等于半径，连结ＯＢ并延长使ＢＣ＝ＯＢ．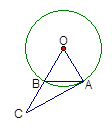
（１）∠ＡＢＣ＝ °；
（２）ＡＣ与⊙Ｏ有什么关系？请证明你的结论；
（３）在⊙Ｏ上，是否存在点Ｄ，使得ＡＤ＝ＡＣ？若存在，请画出图形，并给出证明；若不存在，请说明理由．
在同一间中学就读的李浩与王真是两邻居，平时他们一起骑自行车上学．清明节后的一天，李浩因有事，比王真迟了１０分钟出发，为了能赶上王真，李浩用了王真速度的１.２倍骑车追赶，结果他们在学校大门处相遇．已知他们家离学校大门处的骑车距离为１５千米．求王真的速度．
在－２，－３，４这三个数中任选２个数分别作为点Ｐ的横坐标和纵坐标．
（１）可得到的点的个数为 ；
（２）求过Ｐ点的正比例函数图象经过第二、四象限的概率（用树形图或列表法求解）；
（３）过点Ｐ的正比例函数中，函数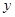
随自变量
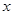的增大而增大的概率为 ．
如图，等腰△ＯＡＢ的顶角∠ＡＯＢ＝３０°，点Ｂ在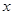
轴上，腰ＯＡ＝４．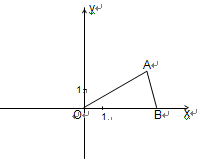
（１）Ｂ点的坐标为： ；
（２）画出△ＯＡＢ关于
轴对称的图形△ＯＡ１Ｂ１（不写画法，保留画图痕迹），求出Ａ１与Ｂ１的坐标；
（３）求出经过Ａ１点的反比例函数解析式．
（注：若涉及无理数，请用根号表示）
先化简，再求值：
，其中
＝－
．