为深化“携手节能低碳，共建碧水蓝天”活动，发展“低碳经济”，某单位进行技术革新，让可再生资源重新利用．今年1月份，再生资源处理量为40吨，从今年1月1日起，该单位每月再生资源处理量每一个月将提高10吨．月处理成本（元）与月份之间的关系可近似地表示为：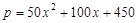
，每处理一吨再生资源得到的新产品的售价定为100元．若该单位每月再生资源处理量为y（吨），每月的利润为w（元）．
（1）分别求出y与x，w与x的函数关系式；
（2）在今年内该单位哪个月获得利润达到5800元？
（3）随着人们环保意识的增加，该单位需求的可再生资源数量受限．今年三月的再生资源处理量比二月份减少了m%，该新产品的产量也随之减少，其售价比二月份的售价增加了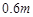
%．四月份，该单位得到国家科委的技术支持，使月处理成本比二月份的降低了
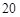%．如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上，其利润比二月份的利润减少了60元，求m的值．
如图， AD平分∠EAC．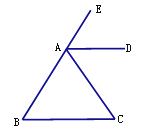
（1）若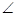
B＝50°AD∥BC，
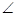则DAC＝°；
（2）若∠C=55°，∠EAC=110°，AD与BC平行吗？
为什么？
根据解答过程填空（填理由或数学式）．
解：∵AD平分∠EAC（已知）
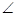∴DAC＝
（）°（角平分线的定义）
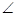∵C＝55°（已知）
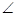∴C＝（） （）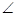
∴AD∥BC（）
如图5，已知线段AB=6，延长线段AB到C，使BC=2AB．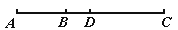
（1）求线段AC的长；
（2）若点D是AC的中点，求线段BD的长．
某校进行校园卫生大扫除，七年级一班原计划分成两个小组，第一组26人打扫大操场，第二组22人打扫班级的包干卫生区．后来根据工作实际需要，要使第二组人数是第一组人数的2倍，那么应从第一组调多少人到第二组？
（1）设应从第一组调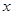
人到第二组，依题意填表（用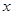的代数式表示）：
| 组别 |
第一组 |
第二组 |
| 原计划小组的人数（单位：人） |
26 |
22 |
| 调整后小组的人数（单位：人） |
（2）根据以上表格列出方程，求出应从第一组调多少人到第二组？
先化简，再求值：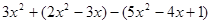
，其中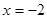
．
化简（第（1）题4分，第（2）题5分，共9分）．
（1）（2x＋1）－（x－1）（2）