在平面直角坐标系xOy中（O为坐标原点），已知抛物线y=x2+bx+c过点A（4，0），B（1，﹣3）．
（1）求b，c的值，并写出该抛物线的对称轴和顶点坐标；
（2）设抛物线的对称轴为直线l，点P（m，n）是抛物线上在第一象限的点，点E与点P关于直线l对称，点E与点F关于y轴对称，若四边形OAPF的面积为48，求点P的坐标；
（3）在（2）的条件下，设M是直线l上任意一点，试判断MP+MA是否存在最小值？若存在，求出这个最小值及相应的点M的坐标；若不存在，请说明理由．
已知O是平面直角坐标系的原点,点A(1,n),B(-1,-n)(n＞0),AB的长是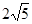
,若点C在
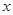轴上,且OC=AC,求点C的坐标．
判断关于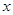
的方程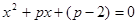
的根的情况．
（1）第一盒乒乓球中有2个白球1个黄球,第二盒子乒乓球中有1个白球1个黄球,分别从每个盒中随机地取出1个球,求这两个球中欧一个是白球一个是黄球的概率；
解方程：
；
（3）如图,在⊙O中,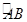
＝
,∠A=30°,求∠B的度数
（1）计算
；
（2）在平面直角坐标系中,已知点A（2,1）,B（2,0）,C（1,-1）,请在图上画出△ABC,并画出与△ABC关于原点O对称的图形；
（3）如图,AB是⊙O的直径,直线AC,BD是⊙O的切线,A,B是切点．求证：AC∥BD．
求代数式
的值是．