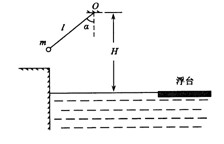
在游乐节目中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，如图所示。我们将选手简化为质量m=50kg的质点，选手抓住绳由静止开始摆动，此时绳与竖直方向夹角
=
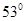，绳长l=2m，绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。（取重力加速度
，
，
）
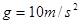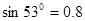（1）求选手摆到最低点时绳子对选手拉力的大小F；
（2）若选手摆到最低点时松手，落到了浮台上，试用题中所提供的数据算出落点与岸的水平距离；
（3）选手摆到最高点时松手落入水中。设水对选手的平均浮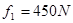力
，平均阻力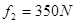
，求选手落入水中的深度
。
某同学的家住在一座30层的高楼内，他每天乘电梯上楼，经过多次仔细观察和反复测量，他发现电梯启动后向上运动的速度符合如下图所示的规律，他就根据这一特点在电梯内用台秤、重物和秒表测量这一楼房的高度。他将台秤放在电梯内，将重物放在台秤的托盘，电梯从第一层开始启动，经过不间断地运行，最后停在第30楼。他测得在第9.5s时台秤的示数为60N，g=10m/s2。求：
（1）电梯启动后在上升过程中台秤的最大示数；
（2）该幢楼房每一层的平均高度（结果保留3位有效数字）。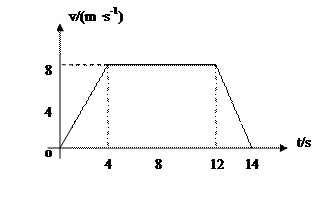
物块（可视为质点）从长为5m、倾角θ=370的固定斜面顶端由静止开始沿斜面下滑，已知物体与斜面之间的动摩擦因数μ=0.3（取g=10m/s2， sin370=0.6，cos370=0.8）。求：
(1)物体滑到斜面底端所需要的时间；
（2）物体到达斜面底端时速度的大小。
如图所示，一个静止在水平地面上A点的物体，质量是2kg，物体与地面之间的动摩擦因数为0.2，物体在大小为20N，方向与水平面成370的斜向下的推力F作用下沿水平地面从A点开始向右沿直线运动，经过2s后撤去外力F，最终物体停在某处B点，求AB之间的总距离（sin370=0.6,cos370=0.8,g=10m/s2结果保留3位有效数字）
一列火车正以8 m/s的速度在水平轨道上做匀速直线运动，突遇紧急情况而刹车，加速度的大小为2m/s2。若从刹车开始计时，求：
（1）火车在第3 s末的速度是；
（2）火车在5 s内的总位移。
某同学手持秒表，在楼顶由静止释放一枚石子，并记录出从释放石子到听到石子落地的时间为3.0s，不计空气阻力和声音传播的时间,g=10m/s2.试求该楼房的高度和石子落地时速度的大小。