某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试中包括形体和口才，笔试中包括专业水平和创新能力考察，他们的成绩（百分制）如下表：
| 候选人 |
面试 |
笔试 |
||
| 形体 |
口才 |
专业水平 |
创新能力 |
|
| 甲 |
86 |
90 |
96 |
92 |
| 乙 |
92 |
88 |
95 |
93 |
（1）若公司根据经营性质和岗位要求认为：形体、口才、专业水平、创新能力按照5：5：4：6的比确定，请计算甲、乙两人各自的平均成绩，看看谁将被录取？
（2）若公司根据经营性质和岗位要求认为：面试成绩中形体占5%，口才占30%，笔试成绩中专业水平占35%，创新能力占30%，那么你认为该公司应该录取谁？
在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构.根据市场调查，这种许愿瓶一段时间内的销售量
（个）与销售单价
（元/个）之间的对应关系如图所示：
（1）观察图象判断与之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润
（元）与销售单价（元/个）之间的函数关系式；
（3）若许愿瓶的进货成本不超过900元，要想获得最大的利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润.
如图，AB是⊙O的直径，直线EF切⊙O于点C， AD⊥EF于点D．
（1）求证：AC平分∠BAD；
（2）若⊙O的半径为2，∠ACD＝30°，求图中阴影部分的面积．（结果保留
）
已知：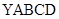
的两边AB、AD的长是关于
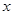的方程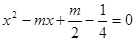
的两个实数根．
（1）当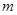
为何值时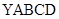，是菱形？求出这时菱形的边长；
（2）若AB=2，那么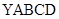的周长是多少？
如图，抛物线
的图象与x轴交于A、B两点，与y轴交于C点，已知点B坐标为（4，0）．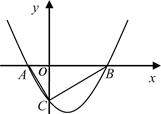
（1）求抛物线的解析式；
（2）判断△ABC的形状，说出△ABC外接圆的圆心位置，并求出圆心的坐标．
如图，四边形ABCD是矩形，对角线AC、BD相交于点O，BE∥AC交DC的延长线于点E．
（1）求证：BD＝BE；
（2）若ÐDBC＝30°，CD＝4，求四边形ABED的面积．