为了防止受到核污染的产品影响我国民众的身体健康，要求产品在进入市场前必须进行两轮核辐射检测，只有两轮都合格才能进行销售，否则不能销售.已知某产品第一轮检测不合格的概率为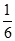
，第二轮检测不合格的概率为
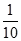，两轮检测是否合格相互没有影响.
（1）求该产品不能销售的概率；
（2）如果产品可以销售，则每件产品可获利40元；如果产品不能销售，则每件产品亏损80元（即获利-80元）.已知一箱中有产品4件，记一箱产品获利X元，求X的分布列，并求出均值E(X).
如图，向量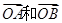
被矩阵M对应的变换
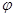作用后分别变成
，
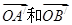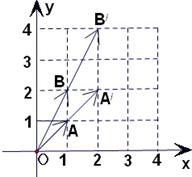
（1）求矩阵M；（2）求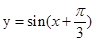
在作用后的函数解析式.
已知函数f(x)=ln(x+1)+ax2-x，a∈R．
（1）当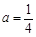
时，求函数y=f(x)的极值；
（2）是否存在实数b∈(0,1)，使得当x∈(-1,b]时，函数f(x)的最大值为f(b)？若存在，求实数a的取值范围，若不存在，请说明理由．
已知曲线C上任意一点P到两定点F1(-1,0)与F2(1,0)的距离之和为4．
（1）求曲线C的方程；
（2）设曲线C与x轴负半轴交点为A，过点M(-4,0)作斜率为k的直线l交曲线C于B、C两点（B在M、C之间），N为BC中点．
(ⅰ)证明：k·kON为定值；
(ⅱ)是否存在实数k，使得F1N⊥AC？如果存在，求直线l的方程，如果不存在，请说明理由．
如图所示，抛物线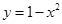
与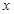
轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在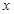轴上.已知工业用地每单位面积价值为
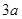元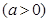
，其它的三个边角地块每单位面积价值
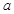元.
（1）求等待开垦土地的面积；
（2）如何确定点C的位置，才能使得整块土地总价值最大.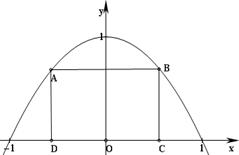
小王经营一家面包店，每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元，若当天卖不完，则未卖出的现烤面包因过期每个亏损5元.经统计，得到在某月（30天）中，小王每天售出的现烤面包个数
及天数如下表：
| 售出个数 |
10 |
11 |
12 |
13 |
14 |
15 |
| 天数 |
3 |
3 |
3 |
6 |
9 |
6 |
试依据以频率估计概率的统计思想，解答下列问题：
（1）计算小王某天售出该现烤面包超过13个的概率；
（2）若在今后的连续5天中，售出该现烤面包超过13个的天数大于3天，则小王决定增加订购量.试求小王增加订购量的概率.
（3）若小王每天订购14个该现烤面包，求其一天出售该现烤面包所获利润的分布列和数学期望.