(本题满分12分,第(Ⅰ)问6分,第(Ⅱ)问6分)已知△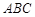 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是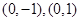 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点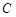 的轨迹
的轨迹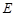 的方程,并判断轨迹
的方程,并判断轨迹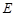 为何种曲线;
为何种曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线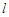 交曲线
交曲线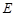 于
于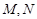 两点,设点
两点,设点 关于
关于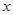 轴的对称点为
轴的对称点为 (
( 不重合)试问:直线
不重合)试问:直线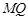 与
与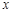 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
物体A以速度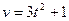 在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以
在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以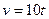 的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s)
的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s)
已知函数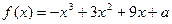
(1) 求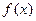 的单调递减区间;
的单调递减区间;
(2) 若f(x)在区间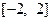 上的最大值为20, 求它在该区间上的最小值.
上的最大值为20, 求它在该区间上的最小值.
(12分)已知等差数列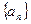 中,前n项和
中,前n项和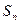 满足:
满足: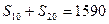 ,
,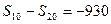 。
。
(Ⅰ)求数列的通项公式以及前n项和公式。
(Ⅱ)是否存在三角形同时具有以下两个性质,如果存在请求出相应的三角形三边
以及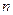 和
和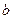 值:
值:
(1)三边是数列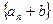 中的连续三项,其中
中的连续三项,其中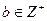 ;
;
(2)最小角是最大角的一半。
(8分)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知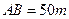 ,
,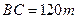 ,于A处测得水深
,于A处测得水深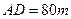 ,于B处测得水深
,于B处测得水深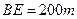 ,于C处测得水深
,于C处测得水深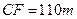 ,求∠DEF的余弦值。
,求∠DEF的余弦值。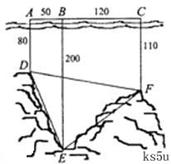
 |
(10分)已知函数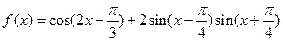
(Ⅰ)求函数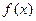 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(Ⅱ)求函数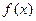 在区间
在区间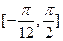 上的值域。
上的值域。