为了了解“通话时长”(“通话时长”指每次通话时间)的分布情况,小强收集了他家1000个“通话时长”数据,这些数据均不超过18(分钟).他从中随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完整的频数分布直方图.
| “通话时长” (x分钟) |
0<x≤3 |
3<x≤6 |
6<x≤9 |
9<x≤12 |
12<x≤15 |
15<x≤18 |
| 次数 |
36 |
a |
8 |
12 |
8 |
12 |
根据表、图提供的信息,解答下面的问题:
(1)a= ,样本容量是 ;
(2)求样本中“通话时长”不超过9分钟的频率: ;
(3)请估计小强家这1000次通话中“通话时长”超过15分钟的次数.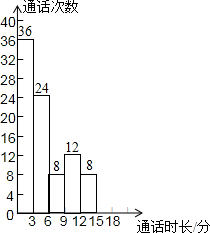
根据提示填空(或填上每步推理的理由)
如图,∠1=∠2,∠3=108°.求∠4的度数。
解:∵∠1=∠2(已知)
∴AB∥CD()
∴∠3+∠4=180°()
∵∠3=108°(已知)
∴∠4=180°-108°=72°
这是一个动物园游览示意图,试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置,(画出图形,并写出各景点的坐标)。 
已知:如图,△ABC,请在图中作出①AB边上的中线CD,②∠BAC的平分线AE,③BC边上的高AF.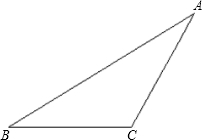
△ABC在如图所示的平面直角坐标系中, 将其平移后得△A′B′C′, 若B的对应点B’的坐标是(4,1).
①在图中画出△A′B′C′;
② 此次平移可看作将△ABC向_____平移了_____个单位长度, 再向_____平移了_____个单位长度得△A′B′C′;
③△A’B’C’的面积为____________. 
京沪高铁是目前世界上一次建成的线路里程最长,技术标准最高的高速铁路,线路全长1320公里。原有京沪铁路全长约1500公里。2011年6月底京沪高铁正式通车,乘坐高铁列车比乘坐普速列车要快10小时36分。已知高铁列车时速是普速列车的3倍,求高铁列车时速。