某商品现在的售价为每件35元.每天可卖出50件.市场调查反映:如果调整价格.每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?
设每件商品降价x元.每天的销售额为y元.
(1)分析:根据问题中的数量关系.用含x的式子填表:
| |
原价 |
每件降价1元 |
每件降价2元 |
… |
每件降价x元 |
| 每件售价(元) |
35 |
34 |
33 |
… |
|
| 每天售量(件) |
50 |
52 |
54 |
… |
|
(2)(由以上分析,用含x的式子表示y,并求出问题的解)
如图, 是 的直径, 是 上两点, 是 的中点,过点 作 的垂线,垂足为 ,连接 交 于点 .
(1)求证: 是 的切线;
(2)若 ,求 的值.

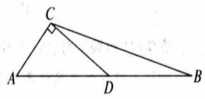
如图,已知 中, 是 的中点, ,求 的值.
如图,在 中, ,作 的垂直平分线交 于点 ,延长 至点 ,使 .
(1)若 ,求 的周长;
(2)若 ,求 的值.

如图甲,在 中, ,如果点 由点 出发沿 方向向点 匀速运动,同时点 由点 出发沿 方向向点 匀速运动,它们的速度均为 .连接 ,设运动时间为 ,解答下列问题:
(1)设 的面积为 ,当 为何值时, 取得最大值, 的最大值是多少?
(2)如图乙,连接 ,将 沿 翻折,得到四边形 ,当四边形 为菱形时,求 的值;
(3)当 为何值时, 是等腰三角形?

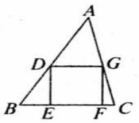
如图,已知锐角 的面积为 ,正方形 是 的一个内接四边形, ,求正方形 面积的最大值.