某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如下图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个开学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量X的平均数和众数;
(2)将Y表示为X的函数;
(3)根据直方图估计利润不少于4800元的概率.
已知椭圆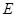 :
: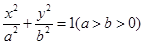 的离心率
的离心率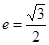 ,并且经过定点
,并且经过定点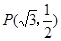 .
.
(1)求椭圆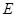 的方程;
的方程;
(2)设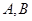 为椭圆
为椭圆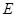 的左右顶点,
的左右顶点, 为直线
为直线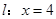 上的一动点(点
上的一动点(点 不在x轴上),连
不在x轴上),连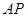 交椭圆于
交椭圆于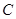 点,连
点,连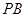 并延长交椭圆于
并延长交椭圆于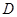 点,试问是否存在
点,试问是否存在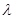 ,使得
,使得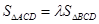 成立,若存在,求出
成立,若存在,求出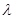 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,已知四棱锥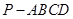 ,底面
,底面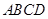 为菱形,
为菱形,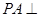 平面
平面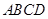 ,
,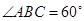 ,
,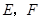 分别是
分别是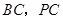 的中点.
的中点.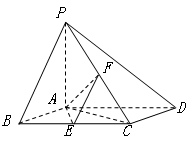
(1)证明: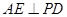 ;
;
(2)若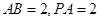 ,求二面角
,求二面角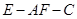 的余弦值.
的余弦值.
已知等差数列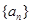 的各项均为正数,
的各项均为正数,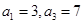 ,其前
,其前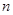 项和为
项和为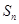 ,
,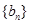 为等比数列,
为等比数列, 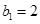 ,且
,且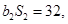 .
.
(1)求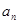 与
与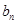 ;
;
(2)若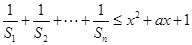 对任意正整数
对任意正整数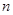 和任意
和任意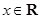 恒成立,求实数
恒成立,求实数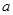 的取值范围.
的取值范围.
已知函数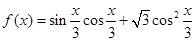 .
.
(1)求该函数图象的对称轴;
(2)在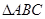 中,角
中,角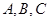 所对的边分别为
所对的边分别为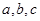 ,且满足
,且满足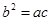 ,求
,求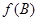 的取值范围.
的取值范围.
已知函数f(x)= +lnx(a>0)
+lnx(a>0)
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)当a=1时,求f(x)在[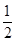 ,2]上的最大值和最小值.
,2]上的最大值和最小值.