如图所示,光滑水平面AB与竖直面的半圆形导轨在B点衔接,导轨半径R,一个质量为m的物块静止在A处压缩弹簧,把物块释放,在弹力的作用下获得一个向右的速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,不计空气阻力,g取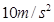 ,求:
,求: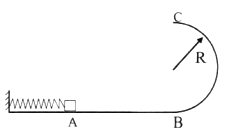
(1)弹簧对物块的弹力做的功;
(2)物块从B至C克服摩擦阻力所做的功;
(3)物块离开C点后落回水平面时动能的大小。
如图所示,真空管内的阴极K发出的电子(不计初速、重力和电子间的相互作用)经加速电压U1加速后,穿过AA'中心的小孔沿中心轴O1 O的方向进入到两块水平正对放置的平行极板P和P'间的区域.当极板P和P'间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;若加上偏转电压U2后,亮点则偏离到O'点.已知电子带电量为-e、质量为m,极板P和P'水平方向的长度为L、极板间距为b,极板右端到荧光屏的距离可忽略不计(如图所示) .求: 
(1)打在荧光屏O点的电子速度的大小
(2)荧光屏上O'点与O点的竖直间距多大
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d = 40cm.电源电动势E = 24V,内电阻r = 1Ω,电阻R = 15Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0 =" 4" m/s竖直向上射入板间.若小球带电量为q = 1×10-2 C,质量为m = 2×10-2 kg,不考虑空气阻力.那么,滑动变阻器接入电路的阻值为多大时,小球恰能到达A板?此时,电源的输出功率是多大?(取g ="10" m/s2)
质谱仪原理如图所示,a为粒子加速器,电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2,今有一质量为m,电量为+e的电子(不计重力),经加速后,该粒子恰能通过速度选择器,粒子进入分离器后做半径为R的匀速圆周运动.
求:(1)粒子的速度v;
(2)速度选择器的电压U2;
(3)粒子在磁感应强度为B2磁场中做匀速圆周运动的半径R.
如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴 和
和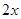 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是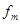 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下, 与
与 、
、 、
、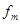 的关系式。
的关系式。
(1)绳中刚出现张力时;
(2)A球所受的摩擦力方向改变时;
(3)两球相对轴刚要滑动时。
一半径为R的雨伞绕伞柄以角速度ω匀速转动,如图所示,伞边缘距地面高为h,甩出的水滴做平抛运动,在地面上形成一个圆,求此圆半径r为多少? 