设函数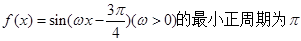
(Ⅰ)求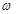 ;
;
(Ⅱ)若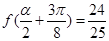 ,且
,且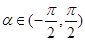 ,求
,求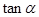 的值.
的值.
(Ⅲ)画出函数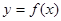 在区间
在区间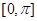 上的图像(完成列表并作图)。
上的图像(完成列表并作图)。
(1)列表
| x |
0 |
|
 |
|
 |
 |
| y |
|
-1 |
|
1 |
|
|
(2)描点,连线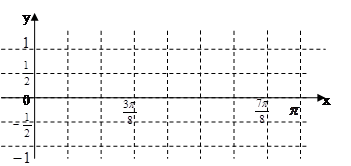
函数f(x) 的定义域为R,且对任意x,y∈R 都有f(x+y)=f(x)+f(y),又
当x>0 时,f(x)<0,且f(1)=-2.
(Ⅰ)求证:f(x) 既是奇函数又是R上的减函数;
(Ⅱ)求f(x)在[-3,3]的最大值和最小值.
在△ABC中, 角A,B,C的对边分别为a,b,c.若 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若sinA,sinB,sinC成等差数列,且ac=36,求b 的值.
若数列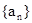 前n项的和
前n项的和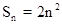 ,数列
,数列 为等比数列,
为等比数列, .
.
(Ⅰ)求数列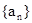 和
和 的通项公式;
的通项公式;
(Ⅱ)若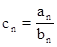 ,求
,求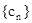 的前n项和
的前n项和 .
.
已知
(Ⅰ)求f(x) 的最小正周期及其图像对称中心的坐标;
(Ⅱ)当 时,求f(x)的值域.
时,求f(x)的值域.
已知: 的定义域为A,
的定义域为A, 的定义域为B。
的定义域为B。
(Ⅰ)求集合A与B;
(Ⅱ)若A∪B=B,求实数a 的取值范围.