已知{an}是正数组成的数列,a1=1,且点(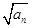 ,an+1)(n∈N*)在函数y=x2+1的图象上.
,an+1)(n∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1=bn+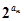 ,
,
求证:bn·bn+2< .
.
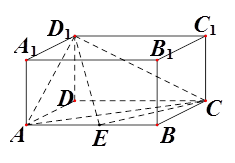
(本题10分)在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)当E为AB的中点时,求点E到平面ACD1的距离;
(2)AE等于何值时,二面角D1-EC-D的大小为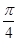 .
.
(本题8分)如图,正三棱柱底面边长为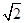 .
.
(1)若侧棱长为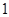 ,求证:
,求证: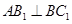 ;
;
(2)若AB1与BC1成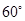 角,求侧棱长
角,求侧棱长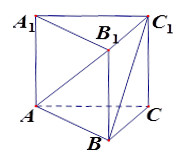
(本题8分)已知直线 被抛物线C:
被抛物线C: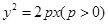 截得的弦长
截得的弦长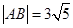 .
.
(1)求抛物线C的方程;
(2)若抛物线C的焦点为F,求三角形ABF的面积.
(本小题满分12分)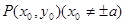 是双曲线
是双曲线 上一点,
上一点,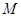 、
、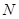 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线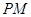 、
、 的斜率之积为
的斜率之积为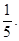
(I)求双曲线的离心率;
(II)过双曲线 的右焦点且斜率为1的直线交双曲线
的右焦点且斜率为1的直线交双曲线 于
于 两点,
两点,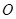 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.
.(本小题满分12分)已知数列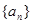 的前n项和为
的前n项和为 ,若
,若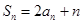 ,且
,且 ,数列
,数列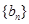 的前n项和为
的前n项和为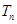 .
.
(I)求证: 为等比数列;
为等比数列;
(Ⅱ)求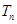 ;
;
(III)设 ,求证:
,求证: