某市为了了解今年高中毕业生的体能情况,从本市某高中毕业班中抽取了一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格,把所得数据进行整理后,分成六组画出频率分布直方图的一部分,如图,已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第六小组的频数是7.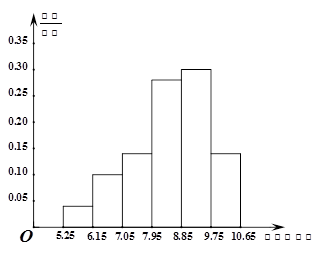
(1)求这次铅球测试成绩合格的人数;
(2)若从第一小组和第二小组中随机抽取两个人的测试成绩,则两个人的测试成绩来自同一小组的概率是多少?
坐标系与参数方程.
在直角坐标系xoy中,直线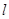 的参数方程为
的参数方程为 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为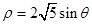 .
.
(1)求圆C的直角坐标方程;
(2)设圆C与直线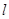 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为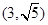 ,求|PA|+|PB|.
,求|PA|+|PB|.
几何证明选讲.
如图,直线 过圆心
过圆心 ,交⊙
,交⊙ 于
于 ,直线
,直线 交⊙
交⊙ 于
于 (不与
(不与 重合),直线
重合),直线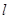 与⊙
与⊙ 相切于
相切于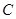 ,交
,交 于
于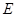 ,且与
,且与 垂直,垂足为
垂直,垂足为 ,连结
,连结 .
.
求证:(1)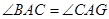 ;
;
(2)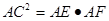 .
.
已知函数,
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;
(3)若 ,使
,使 成立,求实数
成立,求实数 取值范围.
取值范围.
已知函数 ,
,
(1)若x=1时 取得极值,求实数
取得极值,求实数 的值;
的值;
(2)当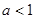 时,求
时,求 在
在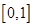 上的最小值;
上的最小值;
(3)若对任意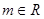 ,直线
,直线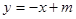 都不是曲线
都不是曲线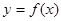 的切线,求实数
的切线,求实数 的取值范围。
的取值范围。
设命题 :函数
:函数 在
在 上为减函数, 命题
上为减函数, 命题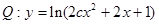 的值域为
的值域为 ,命题
,命题 函数
函数 定义域为
定义域为
(1)若命题 为真命题,求
为真命题,求 的取值范围。
的取值范围。
(2)若 或
或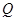 为真命题,
为真命题, 且
且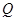 为假命题,求
为假命题,求 的取值范围.
的取值范围.