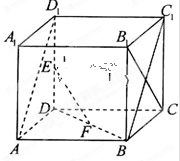
如图所示,在正方体 中,E、F分别为DD1、DB的中点.
中,E、F分别为DD1、DB的中点.
(I)求证:EF//平面ABC1D1;
(II)求证: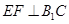 ..
..
(本小题满分10分)
在 中,角
中,角 所对的边分别为
所对的边分别为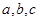 .已知
.已知 ,
, ,
,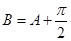 .
.
(Ⅰ)求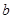 的值;
的值;
(Ⅱ)求 的面积.
的面积.
(本小题满分10分)
等差数列 的前n项和为
的前n项和为 ,已知
,已知 ,
, .
.
(Ⅰ)求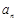 及
及 ;
;
(Ⅱ)令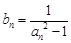 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
(本小题满分14分)
已知数列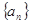 ,
,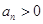 ,其前
,其前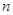 项和
项和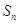 满足
满足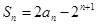 ,其中
,其中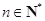 .
.
(Ⅰ)设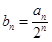 ,证明:数列
,证明:数列 是等差数列;
是等差数列;
(Ⅱ)设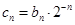 ,
,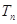 为数列
为数列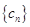 的前n项和,求证:
的前n项和,求证: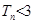 ;
;
(Ⅲ)设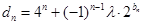 (
(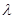 为非零整数,
为非零整数,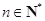 ),试确定
),试确定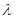 的值,使得对任意
的值,使得对任意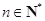 ,都有
,都有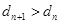 成立.
成立.
(本小题满分12分)
某企业为解决困难职工的住房问题,决定分批建设保障性住房供给困难职工,首批计划用100万元购买一块土地,该土地可以建造每层1000平方米的楼房一幢,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元,已知建筑第1层楼房时,每平方米的建筑费用为920元.为了使该幢楼房每平方米的平均费用最低(费用包括建筑费用和购地费用),应把楼房建成几层?此时平均费用为每平方米多少万元?
(本小题满分12分)
在 ABC中,D是BC上的点,AD平分
ABC中,D是BC上的点,AD平分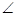 BAC,
BAC, ABD面积是
ABD面积是 ADC面积的2倍.
ADC面积的2倍.
(Ⅰ)求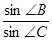 ;
;
(Ⅱ)若 ,求
,求 和
和 的长.
的长.