(本小题满分12分)已知数列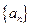 满足
满足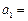
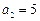 ,
,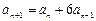 (
(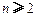 ,
,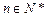 ),
),
若数列 是等比数列.(1)求数列
是等比数列.(1)求数列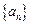 的通项公式;(2)求证:当
的通项公式;(2)求证:当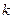 为奇数时,
为奇数时,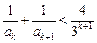 ;(3)求证:
;(3)求证: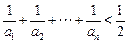 (
(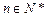 ).
).
已知函数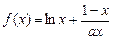 ,其中为大于零的常数.(1)若函数
,其中为大于零的常数.(1)若函数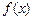 在
在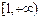 上单调递增,求
上单调递增,求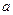 的取值范围;(2)求函数
的取值范围;(2)求函数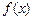 在区间
在区间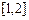 上的最小值;(3)求证:对于任意的
上的最小值;(3)求证:对于任意的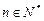 且
且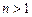 时,都有
时,都有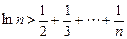 成立.
成立.
已知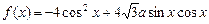 ,将
,将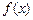 的图象向左平移
的图象向左平移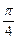 个单位后所得的图象关于
个单位后所得的图象关于 对称.(1)求实数
对称.(1)求实数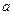 ,并求出
,并求出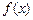 取得最大值时的集合;(2)求
取得最大值时的集合;(2)求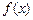 的最小正周期,并求
的最小正周期,并求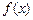 在
在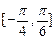 上的值域.
上的值域.
已知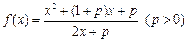
(1)若p > 1时,解关于x的不等式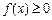 ;
;
(2)若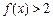 对
对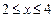 时恒成立,求p的范围.
时恒成立,求p的范围.
数列{an}中a1 = 2,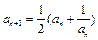 ,{bn}中
,{bn}中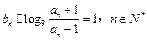 .
.
(1)求证:数列{bn}为等比数列,并求出其通项公式;
(2)当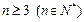 时,证明:
时,证明: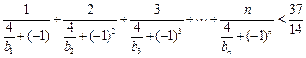 .
.