已知椭圆 :
: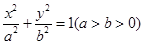 的离心率
的离心率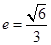 ,
,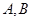 是椭圆
是椭圆 上两点,
上两点,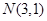 是线段
是线段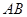 的中点,线段
的中点,线段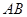 的垂直平分线与椭圆
的垂直平分线与椭圆 相交于
相交于 两点.
两点.
(1)求直线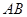 的方程;
的方程;
(2)是否存在这样的椭圆,使得以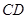 为直径的圆过原点
为直径的圆过原点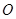 ?若存在,求出该椭圆方程;若不存在,请说明理由.
?若存在,求出该椭圆方程;若不存在,请说明理由.
某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为 ,
, ,
, ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.
(1)求该参加者有资格闯第三关的概率;
(2)求ζ的分布列和数学期望.
如图,在边长为 的正方体
的正方体 中,
中, 、
、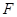 分别是
分别是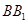 、
、 的中点,试用向量的方法:
的中点,试用向量的方法: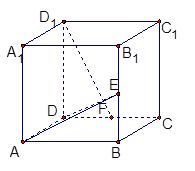
 求证:
求证: 平面
平面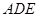 ;
;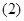 求
求 与平面
与平面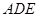 所成的角的余弦值.
所成的角的余弦值.
已知直线 在极坐标系中的方程为
在极坐标系中的方程为 ,圆C在极坐标系中的方程为
,圆C在极坐标系中的方程为 ,求圆C被直线
,求圆C被直线 截得的弦长.
截得的弦长.
求使等式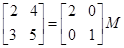 成立的矩阵
成立的矩阵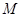 .
.
已知函数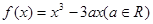
(1)当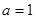 时,求
时,求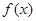 在
在 的最小值;
的最小值;
(2)若直线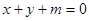 对任意的
对任意的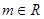 都不是曲线
都不是曲线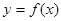 的切线,求
的切线,求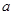 的取值范围;
的取值范围;
(3)设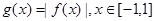 ,求
,求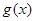 的最大值
的最大值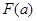 的解析式
的解析式