“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s（千米）与时间t（时）的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题：
(1)小明全家在旅游景点游玩了多少小时？
(2)返程途中小汽车的速度每小时多少千米？请你求出来，并回答小明全家到家是什么时间？
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油
升.
请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
某联欢会上有一个有奖游戏，规则如下：有3张纸牌，背面都是喜羊羊头像，正面有1张是笑脸，其余2张是哭脸．现将3张纸牌洗匀后背面朝上摆放到桌上，若翻到的纸牌中有笑脸就有奖，没有笑脸就没有奖．
（1）小芳获得一次翻牌机会，她从中随机翻开一张纸牌．小芳得奖的概率是．
（2）小明获得两次翻牌机会，他同时翻开两张纸牌．小明认为他得奖的概率是小芳的两倍，你赞同他的观点吗？请用树形图或列表法进行分析说明．
今年，某社区响应泰州市政府“爱心一日捐”的号召，积极组织社区居民参加献爱心活动.为了解该社区居民捐款情况，对社区部分捐款户数进行分组统计（统计表如下）,数据整理成如图所示的不完整统计图.请结合图中相关数据回答下列问题：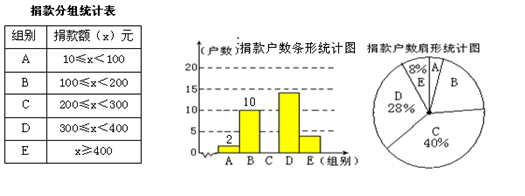
（1）本次调查的样本容量是多少？
（2）求出C组的频数并补全捐款户数条形统计图.
（3）若该社区有1000户住户，请估计捐款不少于200元的户数是多少？
某校为开展“阳光体育”活动，计划拿出不超过3200元的资金增购一批篮球和排球.已知篮球和排球的单价比为9：4，且其单价和为130元.
（1）请问篮球和排球的单价分别为多少元？
（2）若要求购买篮球和排球的总数量为40个，且排球不超过10个，请问有几种购买方案？
计算或化简
（1）计算：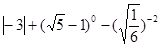
（2）化简：
初一（10）班同学到野外上数学活动课，为测量池塘两点A、B的距离，设计了如下方案：
（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；
（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.
阅读后回答下列问题：
（1）方案（Ⅰ）是否可行？请说明理由。
（2）方案（Ⅱ）是否可行？请说明理由。
（3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是；
若仅满足∠ABD=∠BDE≠90°， 方案（Ⅱ）是否成立？.