为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个2×2列联表:
| |
认为作业多 |
认为作业不多 |
合计 |
| 喜欢玩手机游戏 |
18 |
2 |
|
| 不喜欢玩手机游戏 |
|
6 |
|
| 合计 |
|
|
30 |
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(Ⅲ)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
(本小题满分12分)已知函数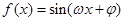
 的一系列对应值如下表:
的一系列对应值如下表:
(Ⅰ)求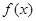 的解析式;
的解析式;
(Ⅱ)在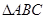 中,若
中,若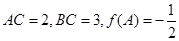 ,求
,求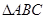 的面积.
的面积.
(本小题满分14分)已知函数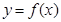 ,
,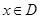 ,设曲线
,设曲线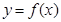 在点
在点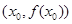 处的切线方程为
处的切线方程为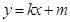 .如果对任意的
.如果对任意的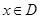 ,均有:
,均有:
①当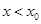 时,
时,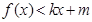 ;
;
②当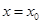 时,
时,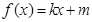 ;
;
③当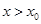 时,
时,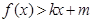 ,
,
则称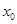 为函数
为函数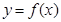 的一个“ʃ-点”.
的一个“ʃ-点”.
(Ⅰ)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
①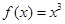 ; ②
; ②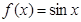 .(只需写出结论)
.(只需写出结论)
(Ⅱ)设函数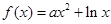 .
.
(ⅰ)若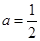 ,证明:
,证明: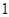 是函数
是函数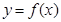 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数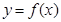 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出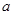 的取值范围.
的取值范围.
(本小题满分13分)已知数列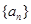 满足
满足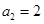 ,
,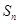 为其前
为其前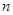 项和,且
项和,且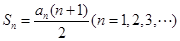 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: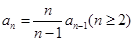 ;
;
(Ⅲ)判断数列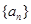 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
(本小题满分14分)已知函数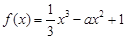 .
.
(Ⅰ)若函数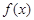 的图象关于点
的图象关于点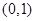 对称,直接写出
对称,直接写出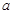 的值;
的值;
(Ⅱ)求函数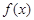 的单调递减区间;
的单调递减区间;
(Ⅲ)若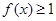 在区间
在区间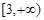 上恒成立,求
上恒成立,求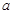 的最大值.
的最大值.
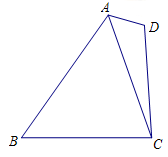
(本小题满分13分)如图所示,在四边形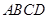 中,
中,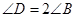 ,且
,且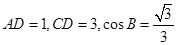 .
.
(Ⅰ)求△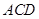 的面积;
的面积;
(Ⅱ)若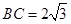 ,求
,求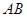 的长.
的长.