已知椭圆 :
: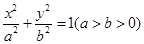 的左焦点
的左焦点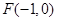 ,离心率为
,离心率为 ,函数
,函数
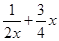 ,
,
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设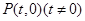 ,
,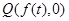 ,过
,过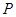 的直线
的直线 交椭圆
交椭圆 于
于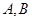 两点,求
两点,求 的最小值,并求此时的
的最小值,并求此时的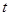 的值.
的值.
(本小题满分14分)关于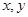 的方程
的方程
(1)若方程C表示圆,求实数m的取值范围;
(2)在方程C表示圆时,若该圆与直线
且 ,求实数m的值;
,求实数m的值;
(3)在(2)的条件下,若定点A的坐标为(1,0),点P是线段MN上的动点,
求直线AP的斜率的取值范围。
(本小题满分14分)已知数列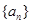 ,
, 满足
满足 ,
,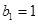 ,且
,且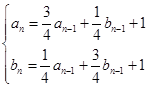 (
( ),
),
数列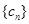 满足
满足
(1)求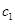 和
和 的值,
的值,
(2)求证:数列 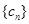 为等差数列,并求出数列
为等差数列,并求出数列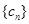 的通项公式
的通项公式
(3)设数列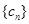 的前
的前 和为
和为 ,求证:
,求证: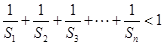
(本小题满分14分)一个几何体是由圆柱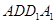 和三棱锥
和三棱锥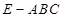 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆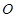 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中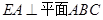 ,
,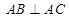 ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥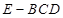 的体积.
的体积.
(本小题满分12分)雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示。
| 男 |
女 |
|
| 文科 |
2 |
5 |
| 理科 |
10 |
3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据: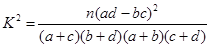
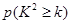 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
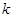 |
2.07 |
2.71 |
3.84 |
5.02 |
6.64 |
7.88 |
10.83 |
(本小题满分12分)如图1,渔船甲位于岛屿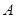 的南偏西
的南偏西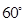 方向的
方向的 处,且与岛屿
处,且与岛屿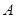 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿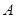 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.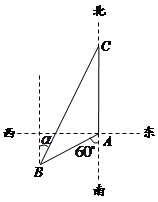
(1)求渔船甲的速度;
(2)求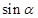 的值.
的值.