某停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时按1小时计算).现有甲、乙两人在该场地停车,两人停车都不超过4小时.
(Ⅰ)若甲停车1小时以上且不超过2小时的概率为 ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲停车付费6元的概率;
,求甲停车付费6元的概率;
(Ⅱ)若甲、乙两人每人停车的时长在每个时段的可能性相同,求甲乙二人停车付费之和为28元的概率.
如图,在底面边长为1,侧棱长为2的正四棱柱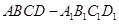 中,P是侧棱
中,P是侧棱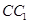 上的一点,
上的一点,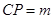 .
.
(1)试确定m,使直线AP与平面BDD1B1所成角为60º;
(2)在线段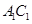 上是否存在一个定点
上是否存在一个定点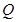 ,使得对任意的m,
,使得对任意的m,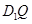 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.
记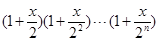 的展开式中,
的展开式中,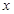 的系数为
的系数为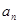 ,
,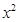 的系数为
的系数为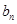 ,其中
,其中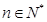
(1)求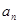 (2)是否存在常数p,q(p<q),使
(2)是否存在常数p,q(p<q),使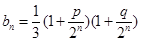 ,对
,对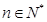 ,
,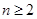 恒成立?证明你的结论.
恒成立?证明你的结论.
某医院有内科医生5名,外科医生4名,现要派4名医生参加赈灾医疗队,
(1)一共有多少种选法?
(2)其中某内科医生甲必须参加,某外科医生乙因故不能参加,有几种选法?
(3)内科医生和外科医生都要有人参加,有几种选法?
定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和两平面的交线平行.
请对上面定理加以证明,并说出定理的名称及作用.
已知:平面α∩平面β=l,α⊥平面γ,β⊥平面γ.
求证:l⊥γ.